| COMPUTATIONAL SIMULATION |
|
 |
|

|
|
|
| Low Frequency Bandgap Characteristics of Three-dimensional Local Resonance Phononic Crystal |
| Nansha GAO,Hong HOU
|
| School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072 |
|
|
|
|
Abstract A kind of three-dimensional local resonance phononic crystal structure was proposed. By FEM calculation, low frequency bandgap characteristic, multiple vibration coupling mechanism and corresponding influence factors of geometric parameters were analyzed. Results show that this kind of structure can open ultra-low frequency bandgap under 50 Hz and critical factor is the vibration coupling effect between the matrix material and cylindrical harmonic oscillator. The more vibration displacement of lower surface on cylindrical harmonic oscillator is, the wider bandgap is. Density of middle oblique bar has no effect on the lower edge of bandgap, but makes the upper edge of bandgap move to the higher frequency range, and hence results in the change of bandgap. Length of middle oblique S2 section and angle of S1 section are the most important factor in bandgap. This study enriches the design and the equivalent model of three-dimensional phononic crystal frequency structure, which possesses a certain guiding value in engineering application.
|
|
Published: 25 January 2018
Online: 2018-01-25
|
|
|
|
|

| Materials | Density/(kg/m3) | Young’s modulus/(1010 Pa) | Shear modulus/(1010 Pa) | Poisson’s ratio | | Lead | 11 600 | 4.08 | 1.49 | 0.369 | | Epoxy resin | 1 180 | 0.435 | 0.159 | 0.368 | | Silicon rubber | 1 300 | 1.175×10-5 | 4×10-6 | 0.469 |
|
|
Parameters of materials
|
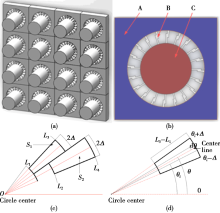
|
|
(a), (b)The structure of three-dimensional local resonance phononic crystal; (c)middle oblique section, (d)local enlarged drawing of middle oblique section
|
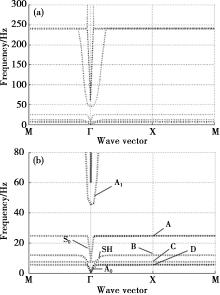
|
|
(a)Band structure of three-dimensional local resonance phononic crystal and (b)local enlarged drawing of band structure (under 80 Hz)
|

|
|
Vibration modal of point A
|

|
|
Vibration modal of point B
|

|
|
Vibration modal of point C
|

|
|
Vibration modal of point D
|

|
|
Vibration modal of point S0
|
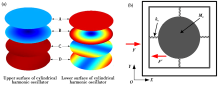
|
|
(a) Displacement comparison between upper and lower surface on cylindrical harmonic oscillator; (b) simple model of local resonance unit
|
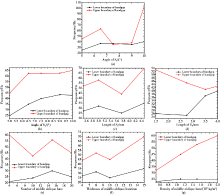
|
|
Effects of (a)S1 angle, (b)S2 angle, (c)S1 length, (d)S2 length, (e)number, (f)thickness and (g)density of middle oblique bars on bandgaps
|
| 1 | Martínez-Sala R, Sancho J, Sánchez J V , et al. Sound attenuation by sculpture[J]. Nature, 1995,378(6554):241. | | 2 | James R, Woodley S M, Dyer C M , et al. Sonic bands, bandgaps, and defect states in layered structures: Theory and experiment[J]. The Journal of the Acoustic Society of America, 1995,97(4):2041. | | 3 | Kushwaha M S, Djafari-Rouhani B, Dobrzynski L . Sound isolation from cubic arrays of air bubbles in water[J]. Physics Letters A, 1998,248(2):252. | | 4 | 4 温熙森, 温激鸿, 郁殿龙 , 等. 声子晶体[M]. 北京: 国防工业出版社, 2009. | | 5 | Liu Z, Zhang X, Mao Y , et al. Locally resonant sonic materials[J]. Science, 2000,289(5485):1734. | | 6 | Liu Z, Chan C T, Sheng P . Three-component elastic wave band-gap material[J]. Physical Review B, 2002,65(16):165116. | | 7 | Liu Z, Chan C T, Sheng P . Analytic model of phononic crystals with local resonances[J]. Physical Review B, 2005,71(1):014103. | | 8 | Hirsekorn M, Delsanto P P, Batra N K , et al. Modelling and simulation of acoustic wave propagation in locally resonant sonic materials[J]. Ultrasonics, 2004,42(1-9):231. | | 9 | Wang G, Shao L H, Liu Y Z , et al. Accurate evaluation of lowest band gaps in ternary locally resonant phononic crystals[J]. Chinese Physics, 2006,15(8):1843. | | 10 | Gan N, Wu J H, Yu L . Research on band gaps in two-dimensional phononic crystal with two resonators[J]. Ultrasonics, 2015,56:287. | | 11 | Qi Pengshan, Du Jun, Jiang Jiulong , et al. Study of the phononic crystals bandgap properties of double local resonance mechanism[J]. Materials Review B:Research Papers, 2016,30(5):144(in Chinese). | | 12 | 祁鹏山, 杜军, 姜久龙 , 等. 双局域共振机制声子晶体带隙特性研究[J]. 材料导报:研究篇, 2016,30(5):144. |
|
|
|
|

 渝公网安备50019002502923号 © Editorial Office of Materials Reports.
渝公网安备50019002502923号 © Editorial Office of Materials Reports.
 2018, Vol. 32
2018, Vol. 32 